728x90

문제 링크 https://www.acmicpc.net/problem/2565
KEY
- 문제에서 없애야 하는 전깃줄의 최소 갯수를 구하라는 말은, 전깃줄의 전체 갯수 - 엉키지 않도록 하는 전깃줄의 최대 갯수를 구하라는 말과 동일하다.
- 입력값의 first를 기준으로 오름차순 정렬을 하면 first를 고정시킬 수 있으므로 second만 고려할 수 있다.
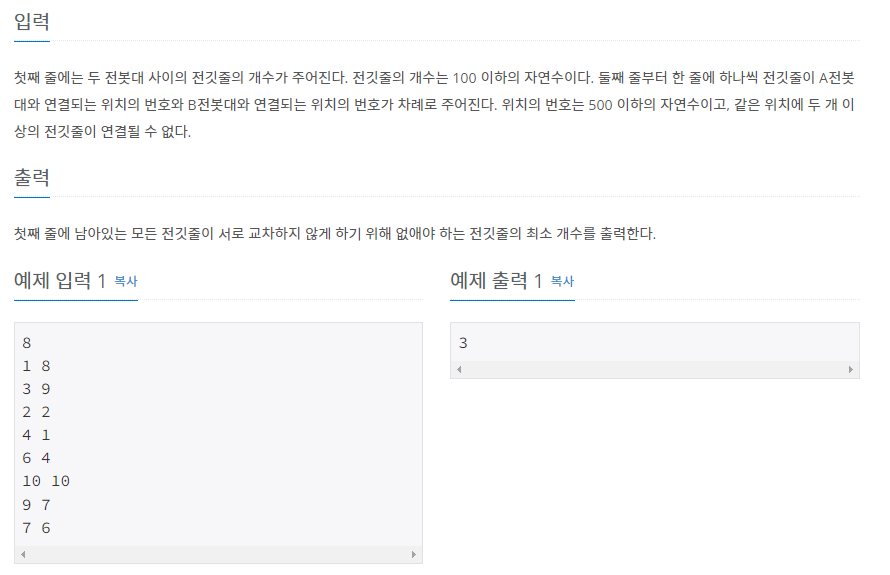
문제의 예제를 살펴보면, 정렬 후 second는 8, 2, 9, 1, 4, 6, 7, 10로 나타난다.
여기서 8, 9, 1을 없앤다면 2,4,6,7,10이 될 것이고, 이는 엉키지 않도록 하는 전깃줄의 최대 갯수가 된다.
따라서, 순열이 주어졌을 때, 가장 긴 증가하는 부분수열의 길이를 구한 후, 전체 갯수 N에서 빼주면 없애야 하는 전깃줄의 최소 갯수가 나올 것이다.
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int MAX = 101;
int n;
vector<pair<int, int>> v;
int dp[MAX] = { 1, }; //부분수열의 길이를 저장하는 배열
int maxValue; //가장 긴 부분수열의 길이
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
int first, second;
cin >> first >> second;
v.push_back({ first,second });
}
//first기준으로 오름차순 정렬
sort(v.begin(), v.end());
//가장 긴 부분수열의 길이(maxValue) 구하기
for (int i = 0; i < n; i++) {
int value = 0;
for (int j = 0; j < i; j++) {
if (v[i].second > v[j].second) {
value = max(value, dp[j]);
}
}
dp[i] = value + 1;
}
for (int i = 0; i < n; i++) {
maxValue = max(maxValue, dp[i]);
}
cout << n - maxValue;
}
|
cs |
728x90
'Algorithm > 동적계획법' 카테고리의 다른 글
| [프로그래머스] 등굣길 c++ (0) | 2023.03.30 |
|---|---|
| [백준] 9251 LCS c++ (0) | 2023.03.29 |
| [백준] 11054 가장 긴 바이토닉 부분 수열 c++ (0) | 2023.03.28 |
| [백준] 11053 가장 긴 증가하는 부분수열 c++ (0) | 2023.03.27 |
| [백준] 1932 정수 삼각형 c++ (0) | 2023.03.26 |




댓글