[양자컴퓨팅] Eigenvectors & Eigenvalues 와 Hermition

😊Eigenvalue & Eigenvector

식 AV = cV를 만족할 때 스칼라c와 벡터V를 각각 A의 eigenvalue, eigenvector라고 한다. 행렬A의 eigenvalue와 eigenvector는 여러개가 있을 수 있다. 아래 예시와 같이 2*2행렬A가 주어졌을 때 (1,2)를 곱하게 되면 2*(1,2)가 나오므로 AV = cV의 형태를 만족하게 된다.  

AV = cV

 

Eigenvector 특징

서로 다른 두 벡터 V와 V'가 있을 때 두 벡터는 같은 eigenvalue c0을 가질 수 있다. 밑의 증명식들은 V대신 다른 것들을 넣었을 때 AV = cV형태로 만들어지면서 같은 c0을 가질 수 있다는 것을 증명하기 위한 것이다.

V대신 cV0를 넣었을 때

 

V대신 cV0 + c'V0을 넣었을 때

 

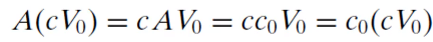
c0을 eigenvalue로 갖는 모든 eigenvector들의 집합은 complex subvector space를 만들고, 이 space를 eigenspace라고 한다.

 

Hermition

n*n행렬 𝐴가 있을 때 𝐴†=𝐴를 만족하는 행렬 A를 Hermition이라고 한다. 즉 어떤 행렬 A를 Transpose하고 Conjugate한 결과가 다시 A가 된다. 예시로 다음 두개의 행렬은 Hermition이다. 

 

Hermition 특징

1. 두 벡터 V, V'를 내적할때, 행렬A를 V에 곱한것의 내적값은 V'에 곱한 것의 내적값과 같다. 

/증명/

 

2. A가 Hermition이라면 모든 eigenvalue는 실수이다.

/증명/

 

3. A가 Hermition이라면 eigenvalues가 다른 eigenvectors간의 내적은 0이다(orthogonal하다).

/증명/

 

Unitary matrix

n*n행렬 U가 있을 때 다음 식을 만족하는 행렬U를 Unitary matrix라고 한다.

 

Unitary matrix 특징

 V와 V'를 내적할 때 각각의 벡터에 U를 곱한 것의 내적은 V와 V'를 내적한 값과 같다.

/증명/

 

Tensor product

두개의 vector space의 곱으로 새로운 vector space를 만들어 내는 연산이다. 기호는 다음과 같이 나타내며, 연산은 밑의 식과 같이 벡터원소 하나에 대해서 다른 벡터의 모든 원소를 곱하여 나타낸다.  

Tensor product 정의

연산 방법