SGD(stochastic gradient descent)
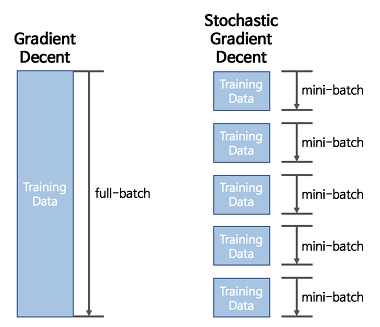
배치 크기가 1인 경사하강법이다. 즉, 전체 데이터가 아닌 랜덤하게 추출된 일부데이터를 사용해서 gradient를 계산하는 방법이다. 일반적인 gradient descent방식(GD)에서 배치는 전체 데이터를 의미하므로 이를 사용하는 것은 노이즈가 적거나 최소값을 얻는데 유용하지만 데이터셋이 커지면 문제가 발생한다. 이 문제는 SGD로 보완할 수 있다.
기존의 너무 느린 GD의 학습방법을 SGD를 통해서 개선했지만, SGD에도 문제가 존재한다. mini-batch를 통해서 학습시키는 경우 최적의 값을 찾아가는 경로는 다음 사진과 같이 뒤죽박죽이다.

따라서 지그재그로 움직이는 비효율적인 경로를 보완하기 위해 모멘텀(Momentum)을 추가한다.
Momentum
모멘텀은 가던 방향을 유지하려는 성질을 뜻하는 관성법칙이다. 모멘텀 + SGD는 이에 따라 한 시점 전의 접선의 기울기값을 일정한 비율만큼 반영해서 지그재그모양을 곡선모양으로 부드럽게 만들 수 있다.

Adagrad
학습률(learning rate)를 너무 높게 잡거나 낮게 잡을 경우 최적값을 찾지 못할 수 있다. 따라서 스텝마다 적절한 learning rate를 적용하는 것이 필요하다. 아래 식을 보면 lr에 h를 곱했다. h는 loss의 변화량에 따라 움직이며, 우리가 처음 학습시키게 될 경우의 loss는 값이 클것이므로 h는 값이 크다. 학습을 해 가면서, 최적의 값을 찾기 직전이라면 반대로 loss 미분값이 작아지므로 h는 작아지게 된다. 따라서 h의 변동에 따라서 적절한 step-size를 구해낼 수 있다.

RMSprop
Adagrad에 이동평균의 개념을 추가한 optimizer이다. 앞서 Adagrad는 적절한 lr을 찾기위해 h를 곱해줬는데, Adagrad도 마찬가지지만 h의 생김새가 살짝 다르다. β와 (1-β)를 각각 h와 ∇loss에 곱해줘서 누적된 평균값을 계산하여 전체적인 추세파악을 쉽게할 수 있다는 장점이 있다.


Adam
모멘텀 + Adagrad의 방식으로, 현재 가장 많이 사용하는 Optimizer이다. 각 파라미터마다 다른 크기의 업데이트를 적용하는 방법이다.

Optimizer 총정리

'Deep Learning' 카테고리의 다른 글
| [DL] 하이퍼파라미터 튜닝 정리 (0) | 2022.05.01 |
|---|---|
| [DL] ANN 활성함수 (Activation function) 종류 (0) | 2022.04.17 |
| [DL] Back-propagation과 Chain Rule (1) | 2022.04.04 |
| [DL] Pytorch을 이용한 모델생성 (0) | 2022.03.28 |
| [DL] 인공신경망에 관련된 개념 정리 (0) | 2022.03.20 |



댓글